깊이 우선 탐색(depth-first search, DFS)
① 깊이 우선 탐색이란?
▷ 그래프의 모든 정점을 발견하는 가장 단순하고 고전적인 방법
▷ 깊이 우선 탐색은 탐색의 각 과정에서 가능한 한 그래프 안으로 '깊이' 들어가려고 시도하며, 막힌 정점에 도달하지 않는 한 뒤로 돌아가지 않습니다.
▷ 깊이 우선 탐색의 중요한 특성은 더 따라갈 간선이 없을 경우 이전으로 돌아간다는 점입니다.
▶ 깊이 우선 탐색 구현할 경우 : 스택(Stack)의 성질 활용(방문하는 순서대로 정점을 스택에 쌓고, 방문이 끝나면 스택에서 pop하는 형태로 구현)
※ DFS : 스택(Stack), BFS : 큐(Queue) 를 사용합니다.
▶ 알고리즘 해결할 경우 : '재귀 호출'을 이용해 해결 (재귀 호출한 함수가 종료하면 호출한 위치로 다시 돌아가기 때문에)
▷ 깊이 우선 탐색은 그래프 전체의 구조를 파악하기 위해 사용되므로, 그래프의 구조상 한 번에 모든 정점을 다 볼 수 없는 경우에도 모든 정점을 다 방문할 필요가 있습니다.
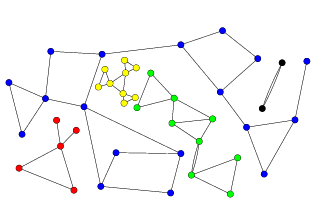
▷ 연결 요소(component)를 컴포넌트라고 읽습니다.
▷ 열결되어 있지 않은 정점은 DFS로 방문할 수 없습니다. 결국 같은 색의 정점들끼리 하나의 컴포넌트를 이룹니다.
▶ DFS 한 번당 하나의 컴포넌트를 방문하므로, 이 때 방문을 시도하는 횟수는 컴포넌트의 갯수가 됩니다.
② 깊이 우선 탐색 시간복잡도?
※ 정점의 집합 : V, 간선의 집합 : E 로 표현합니다.
※ 무방향 그래프(undirected graph) : 간선의 방향이 없어 양 방향으로 이동 가능, 방향그래프(directed graph) : 간선의 방향으로만 이동
▷ 인접리스트 : O (|V| + |E|)
- dfs()는 한 정점마다 한 번씩 호출되므로, 정확히 |V|번 호출합니다.
- 모든 정점에 대해 dfs()를 수행 후, 모든 간선을 정확히 한 번(방향 그래프) 혹은 두 번(무향 그래프) 확인함을 알 수 있습니다.
▷ 인접행렬 : O (|V|²)
- dfs() 호출 횟수는 |V|번입니다.
- 인접 행렬을 사용할 때는 dfs() 내부에서 다른 모든 정점을 순회하며 두 정점 사이에 간선이 있는가를 확인해야 하기 때문에 한 번의 실행에 O (|V|)의 시간이 든다.
③ 깊이 우선 탐색으로 그래프 순회
1번 노드부터 시작하겠습니다.
▷현재 정점 : 1
▷순서 : 1
▷스택 : 1
1번 노드와 인접한 2번,3번 노드 중 더 작은 2번 노드를 선택합니다.
▷현재 정점 : 2
▷순서 : 1 2
▷스택 : 1 2
2번 노드와 인접한 4번,5번 노드 중 더 작은 4번 노드를 선택합니다.
▷현재 정점 : 4
▷순서 : 1 2 4
▷스택 : 1 2 4
4번 노드에서 더이상 들어갈 수 없으므로 2번 노드로 돌아갑니다.
▷현재 정점 : 2
▷순서 : 1 2 4
▷스택 : 1 2
2번 노드에서 아직 들어가지 않은 5번 노드로 들어갑니다.
▷현재 정점 : 5
▷순서 : 1 2 4 5
▷스택 : 1 2 5
5번 노드에서 더이상 들어갈 수 없으므로 2번 노드로 돌아갑니다.
▷현재 정점 : 2
▷순서 : 1 2 4 5
▷스택 : 1 2
2번 노드는 이미 접근을 했기 때문에 1번으로 돌아갑니다.
▷현재 정점 : 1
▷순서 : 1 2 4 5
▷스택 : 1
1번 노드에서 아직 들어가지 않은 3번 노드로 들어갑니다.
▷현재 정점 : 3
▷순서 : 1 2 4 5 3
▷스택 : 1 3
3번 노드와 인접한 6번,7번 노드 중 더 작은 6번 노드를 선택합니다.
▷현재 정점 : 3
▷순서 : 1 2 4 5 3 6
▷스택 : 1 3 6
3번 노드와 인접한 6번,7번 노드 중 더 작은 6번 노드를 선택합니다.
▷현재 정점 : 7
▷순서 : 1 2 4 5 3 6 7
▷스택 : 1 3 6 7
모두 탐색하여 더 이상 갈 곳이 없으므로, 스택을 순서대로 비워줍니다.
▷현재 정점 : 6
▷순서 : 1 2 4 5 3 6 7
▷스택 : 1 3 6
모두 탐색하여 더 이상 갈 곳이 없으므로,스택을 순서대로 비워줍니다.
▷현재 정점 : 3
▷순서 : 1 2 4 5 3 6 7
▷스택 : 1 3
모두 탐색하여 더 이상 갈 곳이 없으므로,스택을 순서대로 비워줍니다.
▷현재 정점 : 1
▷순서 : 1 2 4 5 3 6 7
▷스택 : 1
모두 탐색하여 더 이상 갈 곳이 없으므로,스택을 순서대로 비워줍니다.
▷현재 정점 :
▷순서 : 1 2 4 5 3 6 7
▷스택 :
※탐색 종료
▶최종 방문 경로 : 1 2 4 5 3 6 7
④ DFS 관련 알고리즘 문제
※ 코드 보기를 누르시면 제가 해결한 코드를 보실 수 있습니다.
(백준 1260) DFS와 BFS (https://www.acmicpc.net/problem/1260) [설명] ▷ DFS의 경우 인접리스트를 활용한 방법으로 해결했습니다. |
(백준 11724) 연결 요소의 개수 (https://www.acmicpc.net/problem/11724) [설명] ▷ 컴포넌트의 성질을 활용하여, 인접리스트를 사용한 방법으로 해결했습니다. |
(백준 10451) 순열 사이클 (https://www.acmicpc.net/problem/10451) [설명] ▷ 백준 11724문제와 비슷한 방식으로 해결하면 됩니다. |
(백준 2667) 단지번호붙이기 (https://www.acmicpc.net/problem/2667) [설명] ▷ 2차원 배열의 좌표 계산이 핵심입니다. |
(백준 4963) 섬의 개수 (https://www.acmicpc.net/problem/4963) [설명] ▷ 백준 2267번 단지붙이기 문제와 푸는 방식은 같다. ▷ 주의할 점은 처음에 제공하는 값이 w(너비), h(높이)이므로 2차원배열 생성할 때 new int[h][w]순으로 반대로 넣어주어야 한다. |
참고
- 프로그래밍 대회에서 배우는 알고리즘 문제해결전략
- https://kks227.blog.me/220769870195
'알고리즘 > 알고리즘 개념' 카테고리의 다른 글
| [알고리즘] 유니온 파인드 (Union-Find) (5) | 2018.04.23 |
|---|---|
| [알고리즘] 너비 우선 탐색 (Breadth-first search, BFS) (0) | 2018.04.12 |
| [알고리즘] 완전탐색 (3) | 2018.04.11 |
| [알고리즘] 기본 정렬 알고리즘 (Sorting Algorithm) (0) | 2018.03.21 |
| [알고리즘] 빅오 표기법(Big-O Notation), 시간복잡도, 공간복잡도 (0) | 2018.02.01 |









